Tutorial: An alternative biometric experimental protocol

Purpose

In a previous post, I discussed an exhaustive biometric experimental protocol. This is not only the simpliest way to generate scores for evaluating biometric experiment, but it also makes use of all available biometric samples. However, the downside of this approach is if there are $N$ samples, there will be $N * (N-1)/2$ comparisons. Among these comparisons, the proportion of genuine scores to the impostor ones is roughly $1:N$ so it is growing with $N$ and this can be significant for large $N$. In this article, I discuss an anternative experimental protocol which aims to reduce the number of impostor scores needed, thus reducing the disparaity in the ratio between the number of genuine scores to the impostor ones, without suffering from significant inaccuracy in performance estimation.

Movitations

Suppose we have five sessions of data, so $S=5$ and there are five unique fingerprints, $J$. We shall reserve samples in session 1 as the templates whereas samples in sessions 2 through to 5 as queries. The comparisons can then be arranged in four matrices, each of which is a result of comparing the template in the gallery (aligned in rows) with the probes (aligned across the columns) of sessions 2 through to 5, respectively, as shown below.

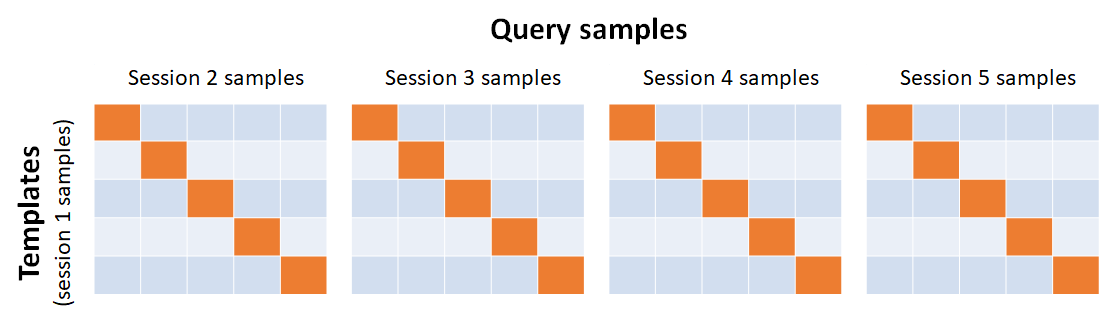
The diagonal elements of each of the four matrices are hence the genuine scores, whereas the off-diagonal elements are the impostor scores. Therefore, the number of genuine scores is: $$J \times (S-1)$$ and the number of impostor scores is: $$\frac 1 2 J (J-1) \times (S-1)$$ So, the genuine to impostor score ratio is $$\frac 1 {J-1}$$ This is still not satisfactory since the ratio changes with increasing number of users (or unique fingers).

One way is to randomly select the impostor samples from all other query sessions (except session one which is reserved as templates). So, we shall harvest all the genuine scores from the matrix but only sub-sample the impostor scores by randomly taking only one of the $S$ sessions. This process is illustrated in the figure below.

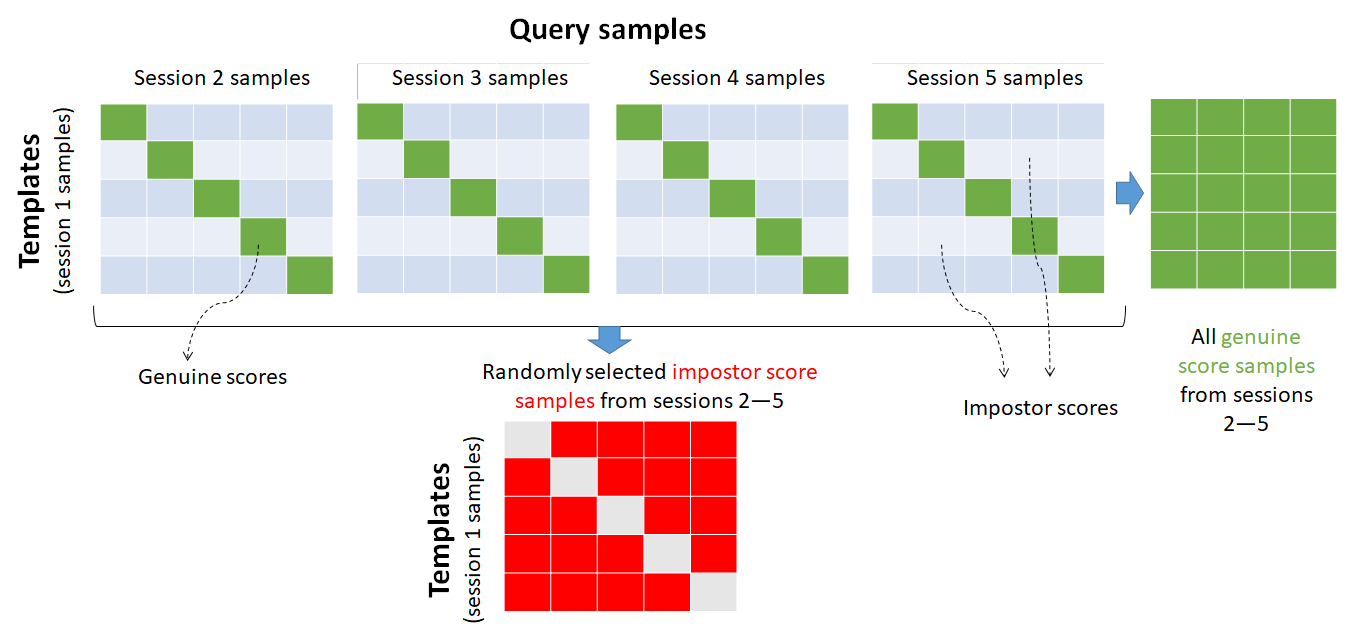
As a result, the number of impostor scores is: $$J \times (J-1)$$ The ratio between the number of genuine scores to the impostor ones is therefore $$\frac{S-1} {J-1}$$

Exercise

Let us continue from the previous tutorial in which 1000 fingerprints have been extracted and are stored in the features directories. We first get the filenames using the code fraction below.

c = 0;
for u=1:200
  for i=1:5
    c=c+1;
    fname{c} = sprintf('features/%d_%d.xyt', u, i); 
  end
end

Write two helper functions.

function out = get_user(x)
  out_ = strsplit(x, '/');
  out_ = strsplit(out_{2}, '_');
  out = str2double(out_{1});
endfunction

function out = get_session(x)
  out_ = strsplit(x, '_');
  out_ = strsplit(out_{2}, '.');
  out = str2double(out_{1});
endfunction

Get the user and session indices

user = cellfun( @(x) get_user(x), fname, "UniformOutput", true);
session = cellfun( @(x) get_session(x), fname, "UniformOutput", true);

Write the query samples to a file.

fid= fopen('queries.tmp', 'w');
cellfun(@(x) fprintf(fid, '%s\n', x), fname(session~=1));
fclose(fid);

The top rows of file queries.tmp contain the following lines.

features/1_2.xyt
features/1_3.xyt
features/1_4.xyt
features/1_5.xyt
features/2_2.xyt
features/2_3.xyt
features/2_4.xyt
features/2_5.xyt
features/3_2.xyt
features/3_3.xyt
...

We shall compare each of these query samples with a list of templates which be definition belong to session 1.

features/1_1.xyt
features/2_1.xyt
features/3_1.xyt
features/4_1.xyt
features/5_1.xyt
...

The following codes achieve this by invoking the NIST fingerprint matcher, bozorth3 in order to obtain the score matrix scores.

templates = fname(session==1);
scores = zeros(numel(templates), sum(session~=1));

for i=1:numel(templates)
  cmd = sprintf("bozorth3 -o out.scores -p %s -G queries.tmp", templates{i});
  tic;
  msg = unix(cmd);
  scores_ = dlmread('out.scores');
  scores(i,:) = scores_;
  time_ = toc;
  fprintf(1, '%d of %d (%1.2f)\n', i, numel(templates), time_); fflush(stdout);
end

We now generate the genuine score mask by using the meta-data user and session which are associated with the list of query samples.

user_list_in_query = user(session~=1); % get session 2,3,4,5
mask_gen = zeros(size(scores));
for i=1:numel(unique(user))
  selected_column = user_list_in_query==i;
  mask_gen(i,selected_column) = 1;
end
mask_imp = 1 - mask_gen;

Let us see how the genuine score matrix look by zooming into the top 20 rows (corresponding to the top 20 unique fingers).

imagesc(scores .* mask_gen);
colorbar;
axis([0.5 80 0.5 20])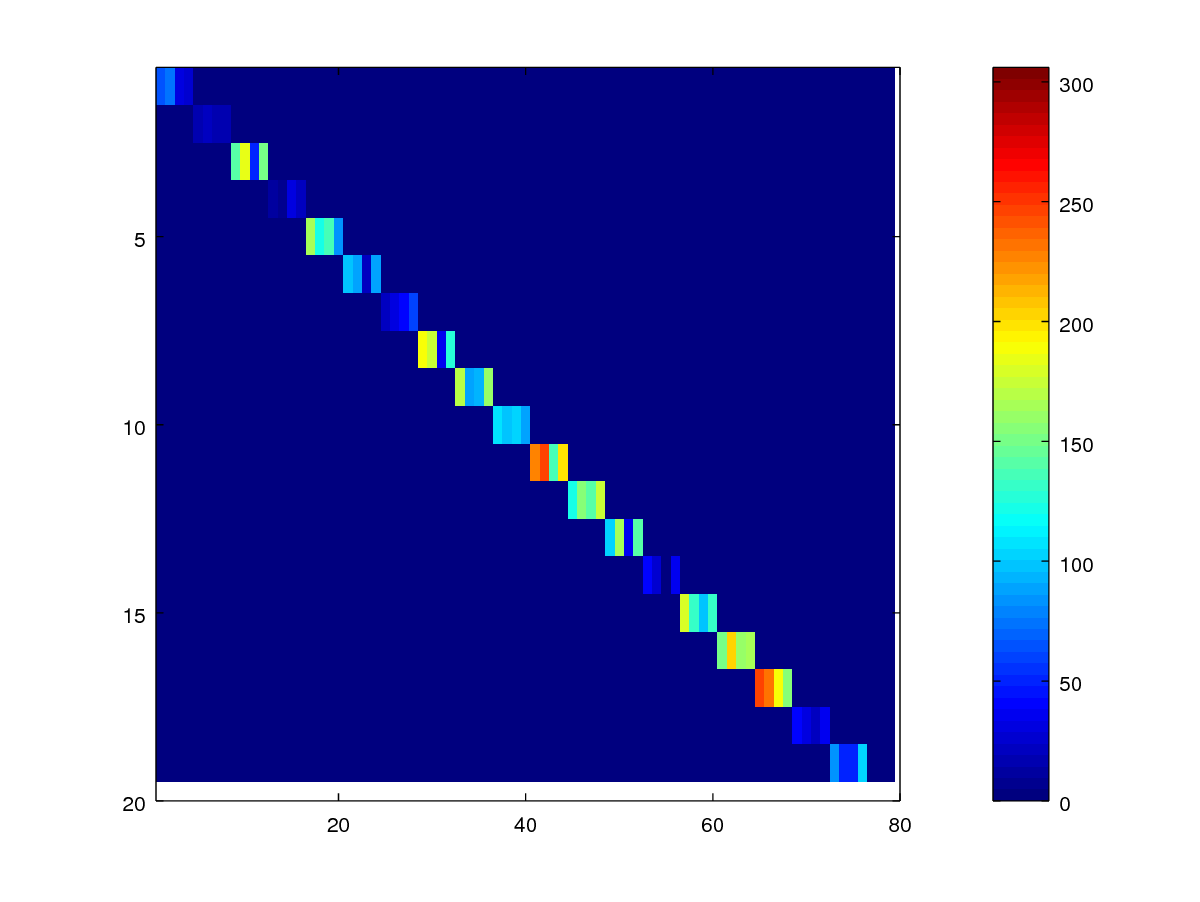

As can be observed, the scores are arranged in the row of consecutive four pixels, corresponding to query samples in session 2, 3, 4, and 5.

Let us plot the masks for the genine and impostor scores, as well as their corresponding score matrices.

subplot(2,2,1);
imagesc(mask_gen);
subplot(2,2,2);
imagesc(mask_imp);
subplot(2,2,3);
gen_scores = scores .* mask_gen;
imagesc(gen_scores);
subplot(2,2,4);
imp_scores = scores .* mask_imp;
imagesc(imp_scores);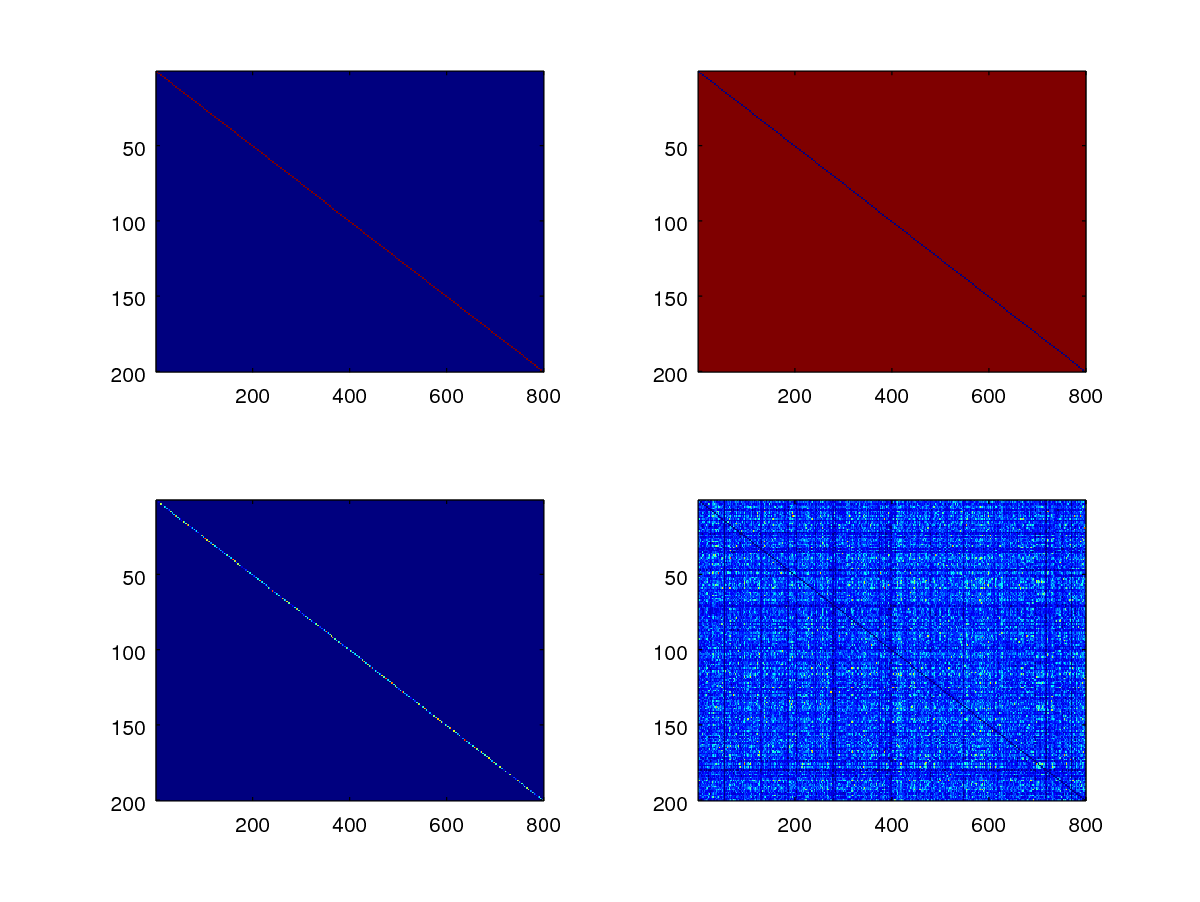

The upper left and right diagrams show where the genuine and impostor score matrices are. The locations are indicated by red pixels (having values of one) against the blue background pixels (having values of zero).

To simply the process, we shall create two helper functions so that you can reuse them in the future. The first one, generate_mask will generate the mask and the second one, get_scores will get the scores given the mask:

function mask_gen = generate_mask(scores, user, session)
  user_list_in_query = user(session~=1);
  mask_gen = zeros(size(scores));
  for i=1:numel(unique(user))
    selected_column = user_list_in_query==i;
    mask_gen(i,selected_column) = 1;
  end
endfunction

function [imp_scores, gen_scores] = get_scores(scores, mask_gen)
  mask_imp = 1 - mask_gen;
  gen_scores = scores(mask_gen==1);
  imp_scores = scores(mask_imp==1);
endfunction

Apply the two functions and plot the various curves using wer.

mask_gen = generate_mask(scores, user, session);
[imp_scores, gen_scores] = get_scores(scores, mask_gen);

%% plot the error rate curve
addpath ../Lib/DETconf/lib/ %to access the wer function
pkg load statistics optim econometrics

eer = wer(imp_scores(:), gen_scores(:),[],1);
fprintf(1,' Equal Error Rate is %1.2f percent\n', eer*100);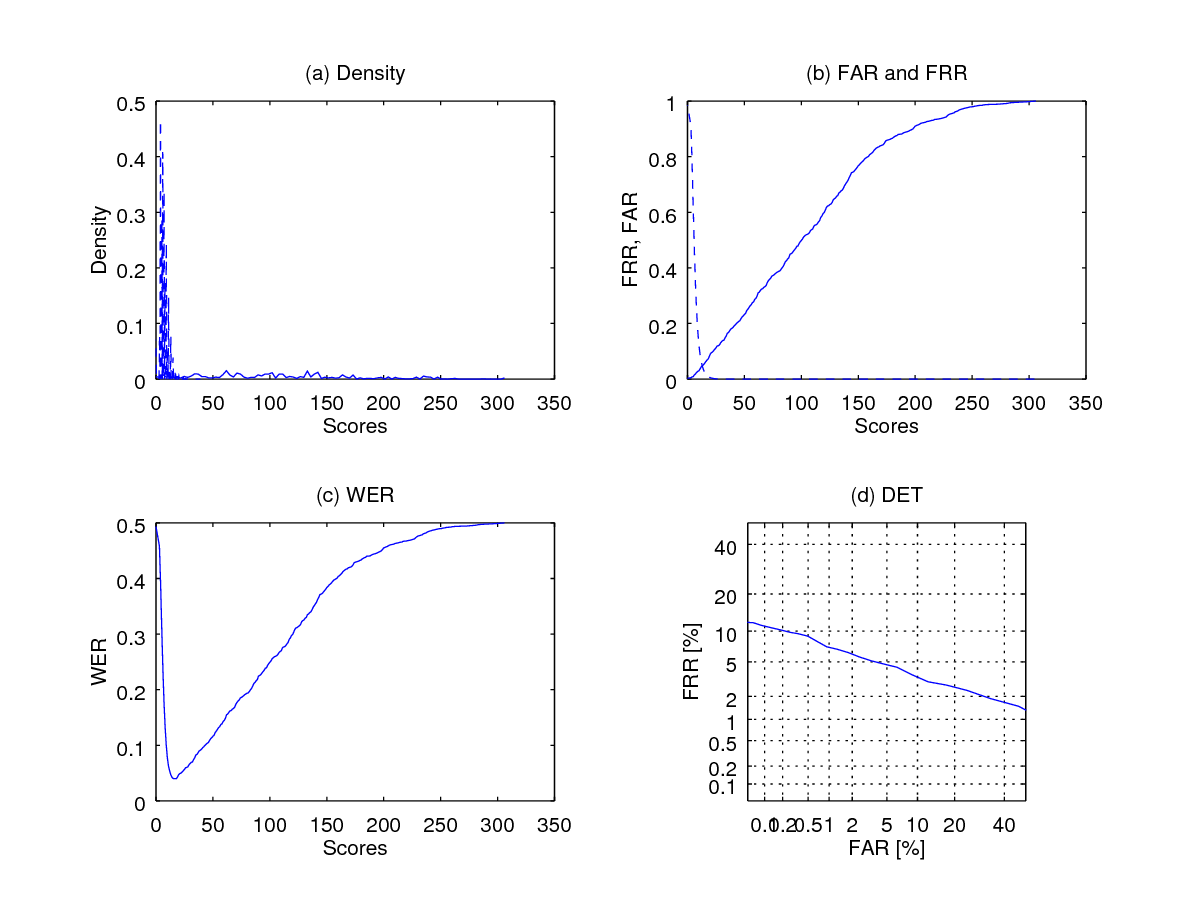

Again, we can do the same using logit_transform, defined below.

function output= logit_transform(scores, max_scores)
  if nargin<2
    max_scores = 400;
  end
  output = log(scores + 1) - log(max_scores - scores) ; %we add one to avoid -Inf
endfunction

Apply logit_transform to the scores so that the distributions becomes more visible before plotting the curves.

eer = wer(logit_transform(imp_scores(:)), logit_transform(gen_scores(:)),[],1);
fprintf(1,' Equal Error Rate is %1.2f percent\n', eer*100);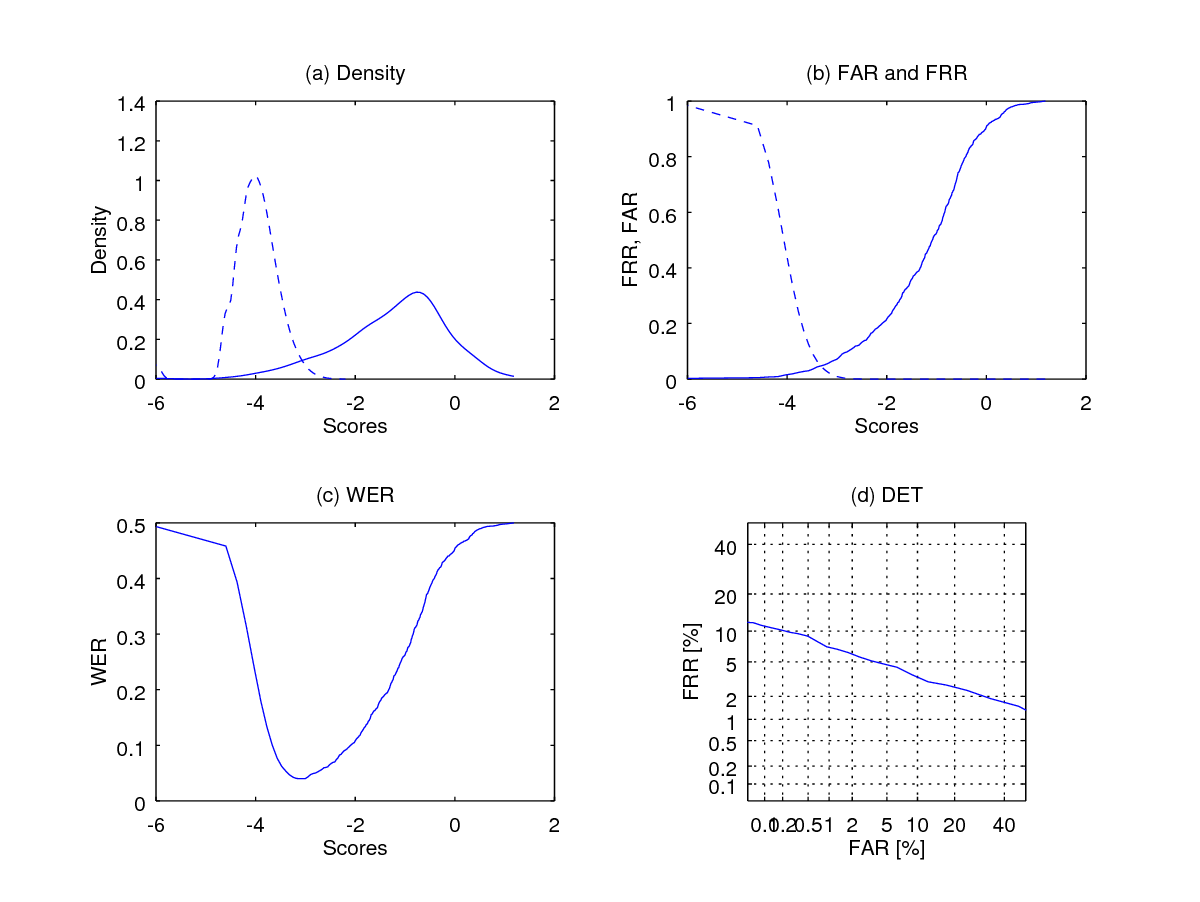

Summary

In this post, I have discussed how to define a biometric experiment protocol such that we need only a minimal number of comparisons. An exhaustive comparison protocol makes $\frac {JS (JS-1)} 2 = O((JS)^2)$ comparisons (in the big O notation), where $J$ is the number of unique fingers and $S$ is the number of samples per unique finger.

A protocol that holds session 1 only samples as templates - single-session template protocol requires $J(S-1) + J(J-1)(S-1) = J (S-1) (J-1) = O(J^2S)$ comparisons.

Finally, an even simplified or minimalist version, or minimalist protocol needs $J(S-1) + J(J-1) = J(J+S -2) = 0(J(J+S))$ number of comparisons which is significantly smaller.

Related Posts

• 01 Feb 2018 » My miscellaneous notes on "coaching for performance"
• 30 Jan 2018 » Biometrics-enabled age verification systems: legal and technological considerations
• 22 Jan 2018 » Installing the Software Demo for Modelling CKD and Detecting AKI

Tags :