January 13, 2018

A Probabilistic Broken-stick Model for CKD Staging and Risk Stratification

Introduction

Determining CKD stage and disease progression based on eGFR in primary care is complicated by the fact that the measurements are irregularly sampled and influenced by both genuine physiological changes and external factors. Models used for these purposes would ideally capture both short- (for staging) and long-term (for progression) trends. However, existing regression algorithms such as linear, polynomial and Gaussian process regression either cannot account for these challenges or do not satisfy the key clinical requirements of providing an easily interpretable model that can elucidate short- and long-term trends. In order to balance interpretability and flexibility, an extension to broken-stick regression models is proposed in order to make them more suitable for modelling clinical time series.

Method

The proposed broken-stick model proceeds by dividing a patient’s eGFR time series into a number of overlapping windows of equal length (although windows can be of different lengths), and then performing a linear regression in each window. These locally linear line segments are then smoothly joined using a Bayesian approach, whereby the further away from a point in time $t$ a windows is the less influence its line segment has near $t$ . This is achieved by defining the posterior probability of the $w$ -th window at time $t$ , i.e., $P(w|t)$ as proportional to $p(t|w)$ , where the window function $p(t|w)$ is bell-shaped, e.g. Gaussian.

In order to demonstrate the utility of this proposed broken-stick model, we used it to model the long term trend of eGFR measurements from the primary care data of 12,000 patients collected as part of the QICKD study. Rather than rely on the raw eGFR values to determine the stage of a patient’s CKD, we used the estimated mean eGFR value obtained directly from the broken-stick model. In addition, by calculating both the expected eGFR value ( $\mu$ ) and slope ( $\mu\prime$ ) at a given time it is possible to stage and stratify patients according to the trajectory that their condition is taking.

Results

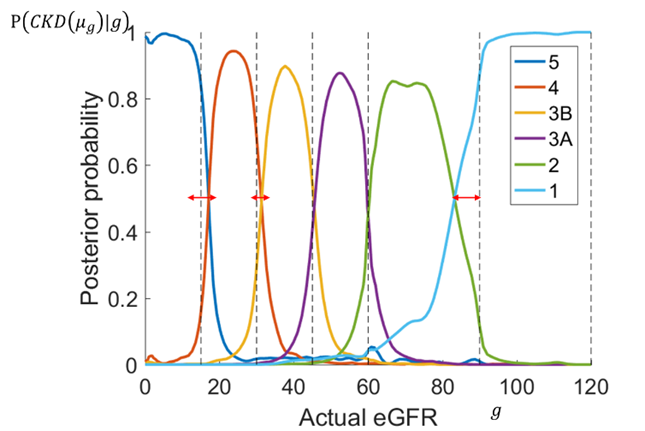
In addition to using the broken-stick model to determine CKD stages, it is possible to both stage and stratify patients according to the trajectory that their condition is taking. From figure a we can see that using expected eGFR slope enables both the staging and trajectory of a patient’s eGFR measurements to be taken into account, and allows us to stratify patients into categories dependent on their current eGFR and the expected trajectory of it. The broken-stick model also enables the calculation of the expected CKD stage posterior, as shown in figure b. Gaps found between the KDIGO guideline stage (dashed vertical lines) and the boundary between expected CKD stages can be interpreted as indicative of systemic variation in recording of patient data compared to what would be expected.

Figure a

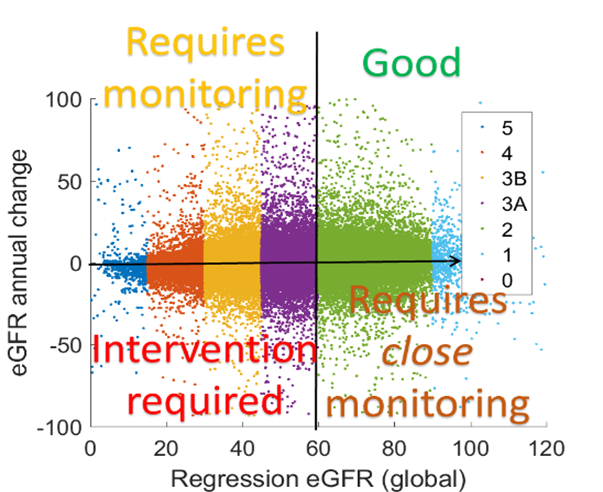
eGFR Stratification

Figure b

eGFR staging

Conclusion

The proposed broken-stick model can robustly estimate both short-term and long-term trends simultaneously, while also accommodating the unequal length and irregularly sampled nature of eGFR time series. While CKD staging is currently based on local trends (the most recent measurements), by modelling a patient’s eGFR time series using a broken-stick model it is possible to base a patient’s stage on their entire time series. Conversely, the broken-stick model enables CKD progression estimates to be based on both short- and long-term trends. CKD stages determined using the broken-stick model are largely consistent with those determined using the KDIGO guidelines, and therefore estimates of progression are likely to prove reliable as they are based on the same model. Taken together, these results could provide useful information when determining the trajectory of a patient’s condition (which allows for early intervention) and in the retrospective identification of patients for clinical research.

What’s next?

To find out more about the broken stick model, you can:

Download the BRS2017 abstract here
Read the poster
Find out more about the algorithm by reading the author’s version of the journal paper or from Science direct

Cite this blog post

Bibtex

    @misc{ poh_2018_01_13_BRS2017-broken-stick-model,
      author = {Norman Poh},
      title = { A Probabilistic Broken-stick Model for CKD Staging and Risk Stratification },
      howpublished = {\url{ http://normanpoh.github.com/blog/2018/01/13/BRS2017-broken-stick-model.html},
      note = "Accessed: ___TODAY___"
    }

Poh, Norman. "A Probabilistic Broken-stick Model for CKD Staging and Risk Stratification". Norman Poh's Github Blog, 2018. http://normanpoh.github.com/blog/2018/01/13/BRS2017-broken-stick-model.html . Accessed .

Poh, Norman (2018). "A Probabilistic Broken-stick Model for CKD Staging and Risk Stratification". Norman Poh's Github Blog, http://normanpoh.github.com/blog/2018/01/13/BRS2017-broken-stick-model.html . Accessed .